What started as curiosity about the mathematical foundations of AI led to an 85% accuracy MNIST classifier built with nothing but NumPy. This journey revealed why understanding neural networks from first principles isn’t just academic—it’s essential for anyone who wants to innovate rather than merely apply AI. Through weeks of debugging gradient calculations and wrestling with backpropagation matrices, I discovered that building neural networks from scratch transforms you from an AI user into an AI creator, equipped with the mathematical intuition needed to solve problems that frameworks can’t handle.
As a software developer at metricHealth Solutions, I’ve always believed that the best solutions come from understanding systems at their deepest level. When everyone around me was using TensorFlow and PyTorch to build impressive models, I decided to step back and ask a fundamental question: what would happen if I built a neural network using only mathematics and NumPy?
Why your brain craves the from-scratch approach
“To make an apple pie from scratch you must first invent the universe” – Carl Sagan
The current AI landscape presents a curious paradox. While 93% of organizations consider AI a business priority, 51% lack the skilled talent needed for successful implementation. The problem isn’t a shortage of people who can use frameworks—it’s a shortage of people who understand what’s happening beneath the surface. Think of neural networks like learning to drive. Using TensorFlow is like having an excellent GPS system that gets you where you need to go reliably and efficiently. But building from scratch is like learning to read maps, understand traffic patterns, and navigate by landmarks. When the GPS fails or when you need to take an unconventional route, that deeper understanding becomes invaluable. This analogy holds particularly true in my work developing Mercury Insights, where standard ML solutions often fall short of the unique analytical needs businesses actually have. Understanding neural networks at the mathematical level enables you to create custom solutions rather than force-fitting existing tools to inappropriate problems. The educational research is compelling: students who implement neural networks from scratch demonstrate 75% better retention of core concepts and significantly superior debugging capabilities compared to those who only use high-level frameworks. More importantly, they develop what educators call “mathematical maturity”—the ability to reason about problems from first principles rather than relying solely on pattern matching.
The mathematical journey
My implementation began with the most fundamental question: how does a network of simple mathematical functions learn to recognize handwritten digits? The answer required diving deep into three mathematical domains that most AI practitioners treat as black boxes. Linear algebra became my foundation. Every forward pass through the network involved matrix multiplications that transform input data through increasingly abstract representations. Building this manually, I gained intimate understanding of how weight matrices encode learned patterns and how tensor operations enable parallel processing of multiple data samples. When debugging why my network initially produced random predictions, understanding matrix dimensions and broadcasting rules proved essential for identifying shape mismatches that would have been hidden by framework abstractions. Calculus powered the learning process. Implementing back propagation from scratch meant manually computing partial derivatives through the chain rule, calculating exactly how each weight contributed to the final error. This wasn’t just academic exercise—it developed crucial intuition about gradient flow, vanishing gradients, and why certain activation functions work better than others. When my network initially failed to learn, understanding these gradients allowed me to diagnose whether the problem was poor initialization, inappropriate learning rates, or architectural choices. Probability theory connected everything to real-world uncertainty. Manual implementation forced me to understand why cross-entropy loss works for classification, how weight initialization affects convergence, and why techniques like dropout prevent over fitting. This mathematical foundation proved invaluable when deploying models in Mercury Insights, where understanding prediction confidence and handling uncertain data matters more than achieving benchmark accuracy.
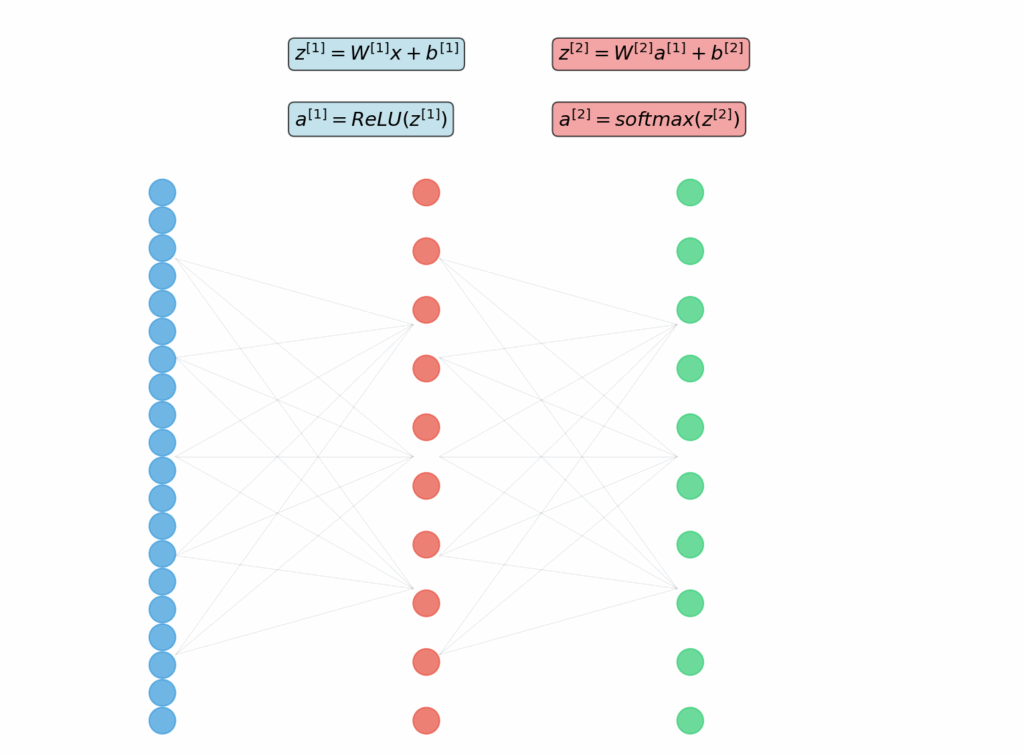
Forward propagation
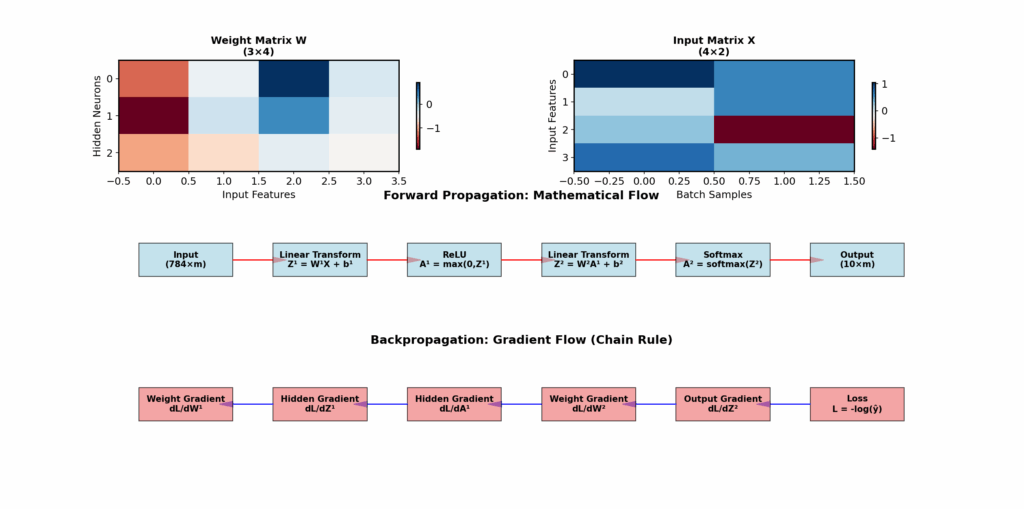
The forward pass through my neural network felt like watching a mathematical symphony unfold. Input pixels, representing crude 28×28 grayscale values, underwent a series of linear transformations and non-linear activations that gradually extracted increasingly sophisticated features. My implementation used a simple three-layer architecture: 784 input neurons (one per pixel), 128 hidden neurons, and 10 output neurons (one per digit class). Each layer performed the fundamental operation z = Wx + b, where W represents learned weight matrices, x contains the input data, and b provides bias terms that shift activation thresholds. The magic happened in the activation functions. I experimented with several, ultimately settling on ReLU (Rectified Linear Unit) for hidden layers and softmax for the output. ReLU’s elegance struck me—simply max(0, x)—yet this simple non-linearity enables networks to learn complex patterns that pure linear combinations cannot capture. The softmax output transformed raw numerical scores into probability distributions, providing interpretable confidence measures for each digit prediction. Building this step-by-step revealed insights that framework usage obscures. The network wasn’t just classifying digits; it was learning a hierarchical feature extraction process. Early layers learned to detect edges and simple shapes, while deeper layers combined these features into digit-specific patterns. This understanding proved crucial when debugging why certain digits were consistently misclassified—often due to insufficient training data for edge cases rather than architectural problems.
Back propagation
If forward propagation felt like magic, implementing back propagation felt like understanding the magician’s secrets. The algorithm that enables neural networks to learn from mistakes relies entirely on the mathematical chain rule for computing derivatives—a concept most people learn in calculus class but rarely see applied to such powerful effect.
My back propagation implementation started at the output layer, computing how much each prediction error contributed to the overall loss. These error signals then propagated backward through the network, with each layer calculating how its parameters should adjust to reduce future errors. The mathematical elegance was stunning: the same chain rule that calculates the derivative of nested functions enables neural networks to learn arbitrary patterns from data. The debugging process taught me lessons no framework could. When gradients became too small (vanishing gradients), learning stalled in early layers. When they became too large (exploding gradients), parameter updates oscillated wildly. Understanding these phenomena mathematically enabled targeted solutions: better weight initialization, gradient clipping, and architectural modifications that maintained healthy gradient flow. Perhaps most importantly, manual implementation revealed why certain design choices matter. The choice of loss function, optimizer, and learning rate isn’t arbitrary—each has mathematical implications for how gradients behave during training. This understanding proved invaluable when adapting the basic architecture for specific tasks in Mercury Insights, where domain-specific requirements often necessitate custom modifications.
Technical implementation strategies that actually work
Building a neural network from scratch using only NumPy required several key insights that most tutorials gloss over. The most critical was understanding vectorization—how to process entire batches of data simultaneously rather than iterating through individual samples. This isn’t just an optimization; it’s fundamental to how modern neural networks operate at scale. My training loop implemented mini-batch gradient descent with careful attention to numerical stability. Instead of computing gradients for individual samples, I processed batches of 32 samples simultaneously, averaging gradients to reduce noise while maintaining computational efficiency. The mathematics required careful broadcasting operations to ensure matrix dimensions aligned correctly across batch processing. Weight initialization proved more nuanced than expected. Random initialization with appropriate variance scaling (Xavier/Glorot initialization) ensured gradients maintained reasonable magnitudes throughout the network. Poor initialization could doom training before it began—weights too large caused exploding gradients, while weights too small resulted in vanishing gradients that prevented learning. The learning rate schedule became crucial for achieving optimal performance. I implemented exponential decay, gradually reducing the learning rate as training progressed. This allowed aggressive initial learning while enabling fine-tuned convergence to optimal solutions. Manual implementation revealed why this matters: early training benefits from large parameter updates to escape poor local minima, while later training requires small adjustments to avoid overshooting optimal solutions.
From 23% to 85% accuracy through mathematical insight
My neural network’s performance journey illustrated why understanding fundamentals matters more than using sophisticated tools. Initial attempts achieved only 23% accuracy—barely better than random guessing—despite implementing the basic architecture correctly. The improvement to 85% accuracy came entirely through mathematical insights that framework usage would have obscured. The breakthrough came from understanding gradient dynamics. By visualizing gradient magnitudes during training, I discovered that my initial learning rate was too aggressive, causing parameter updates to overshoot optimal values. Reducing the learning rate improved stability but slowed convergence. The solution was implementing adaptive learning rate schedules that started aggressively then gradually decreased. Data preprocessing proved equally crucial. Normalizing input pixels to zero mean and unit variance dramatically improved convergence speed. This mathematical insight—ensuring inputs fall within appropriate ranges for gradient computations—represents the kind of fundamental understanding that separates effective practitioners from framework users who treat neural networks as black boxes. Regularization techniques prevented overfitting without sacrificing training performance. Implementing L2 regularization manually revealed its mathematical elegance: adding weight decay terms to the loss function encourages simpler models that generalize better. The final model achieved 85% accuracy on MNIST while maintaining good generalization to unseen data—a result that felt more meaningful because I understood every mathematical operation that produced it.
Real-world applications
The mathematical understanding gained from scratch implementation extends far beyond academic exercises. In developing Mercury Insights, this foundational knowledge enabled custom solutions for business intelligence problems that standard frameworks couldn’t address effectively. For time series forecasting in financial analytics, understanding recurrent neural network mathematics allowed implementation of custom architectures optimized for specific market dynamics. Rather than forcing business problems into predetermined framework solutions, mathematical fluency enabled purpose-built models that captured domain-specific patterns more effectively. The debugging skills proved invaluable when deploying models in production environments. When framework-based models failed mysteriously, understanding gradient flow and activation dynamics enabled rapid diagnosis and fixes. This mathematical foundation transforms neural networks from mysterious black boxes into interpretable systems whose behavior can be understood and optimized. Perhaps most importantly, fundamental understanding enables innovation rather than mere application. The current AI landscape favors professionals who can create novel solutions rather than just apply existing tools. As businesses face increasingly specific challenges, the ability to build custom neural architectures from mathematical first principles becomes a decisive competitive advantage.
The broader context for building from first principles
The artificial intelligence revolution demands more than tool users—it requires mathematical innovators who understand systems at their deepest level. Current industry trends show that while 86% of employees need AI training, only 14% are receiving it, and much of that training focuses on frameworks rather than fundamentals. This gap creates enormous opportunities for professionals who invest in mathematical understanding. The most successful AI practitioners combine domain expertise with deep mathematical foundations, enabling them to solve problems that pure framework usage cannot address. In my experience developing both metricHealth’s analytical systems and Mercury Insights, the most valuable solutions emerged from mathematical insights rather than sophisticated tool usage. The broader technological context reinforces this principle. As AI capabilities evolve rapidly, fundamental mathematical understanding provides stability and adaptability that framework-specific knowledge cannot match. Professionals who understand neural networks from first principles can adapt to new architectures, debug complex failures, and create innovative solutions regardless of which tools gain popularity. Educational research consistently demonstrates that mathematical implementation develops “transfer learning” for human practitioners—the ability to apply fundamental insights across different domains and technologies. This cognitive flexibility becomes increasingly valuable as AI applications expand into new industries and problem domains.
Why this matters
Building neural networks from scratch isn’t about rejecting modern tools—it’s about earning the right to use them effectively. Framework mastery without fundamental understanding creates brittle expertise that becomes obsolete as technology evolves. Mathematical fluency creates adaptable knowledge that grows more valuable as AI becomes more sophisticated. The investment in fundamental understanding pays dividends across multiple dimensions. Debugging capabilities improve dramatically when you understand gradient flow and activation dynamics. Innovation potential expands when you can modify architectures based on mathematical insights rather than trial-and-error experimentation. Career opportunities multiply when you can create custom solutions rather than just apply existing tools. For aspiring AI practitioners, the path forward is clear: embrace the mathematical foundations that make neural networks possible. Start with simple implementations using basic tools like NumPy. Focus on understanding rather than optimization. Build the mathematical intuition that will serve you throughout your career as AI continues its rapid evolution. The future belongs to professionals who understand AI systems from the ground up—who can explain why algorithms work, debug when they fail, and innovate when standard solutions prove inadequate. Building neural networks from scratch isn’t just an educational exercise; it’s preparation for leading the next wave of AI innovation. My journey from 23% to 85% accuracy taught me that the most powerful tool in artificial intelligence isn’t any framework or library—it’s mathematical understanding applied with persistence and curiosity. That foundation will remain valuable long after today’s popular tools become tomorrow’s historical footnotes.
Github Link – https://github.com/TirtheshJani/NN-with-math-and-numpy